PSLE Math Revision: Whole Numbers

🧮 Constant Difference

✅ Concept: When the difference between two quantities stays the same even after changes (e.g. both increase or decrease by the same amount), we use the Constant Difference method.

💡 Tip:

• Useful for solving word problems with same increase/decrease.
• Use when both parties change by the same amount.

---

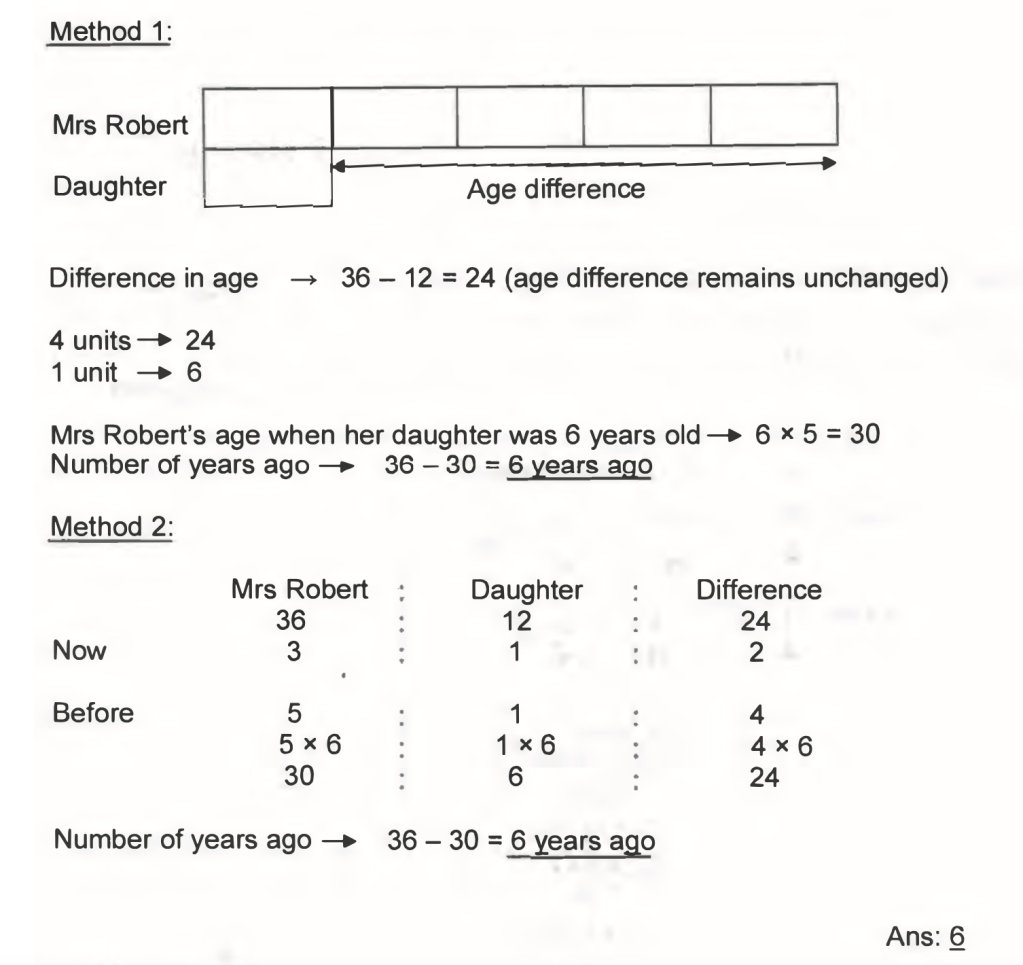
🧩 Example Problem:

Mrs Robert is 36 years old and her daughter is 24 years younger.
How many years ago was Mrs Robert five times as old as her daughter?

---

🧠 Step-by-Step Breakdown:

When a question involves a comparison of ages and phrases like “How many years ago…”, think:
👉 Constant Difference strategy.

That means:
✅ The age gap never changes.
✅ Only time moves forward or backward equally for both.

🧮 Proportion / Grouping

✅ Concept: Use this when items or people are grouped equally or compared in ratios.

💡Tip:

• Look for words like “each”, “per group”, “shared equally”.
• Sometimes involves ratio or unitary method.

---

🧩 Example Problem:

For a school charity sale, every girl was given 5 tickets to sell and every boy was given 3 tickets to sell.
There were thrice as many girls as boys at the sale.
If a total of 576 tickets were sold, how many girls were at the charity sale?

---

🧠 Step-by-Step Breakdown:

When you see keywords like:

• “Every boy/girl gets ___”
• “There are ___ times as many of one group as another”
• “Total = ___”
  👉 You’re in Grouping and Proportion territory!

–

🧮 More Than / Less Than (with internal transfer)

✅ Concept: Involves transfer of items between two parties. The total stays the same, but one has more/less than before.

💡Tip:

• Great for “equal number” after giving/sharing problems

---

🧩 Example Problem:

The number of marbles in container A was 36 more than that in container B.
When 48 marbles were removed from container A and placed in container B, the number of marbles in container B became thrice that of container A.
Find the number of marbles in container A at first.

---

🧠 Step-by-Step Breakdown:

When you see phrases like:

“Internal transfer” = giving between two people, no new items added

Use difference ÷ 2 to balance

• “A had more than B”
• “Then marbles were moved from A to B”
• “Now B has ___ times A”
  👉 It’s time to use internal transfer logic – no marbles were lost, just moved!

🧮 More Than / Less Than (with comparison at two points)

✅ Concept:

Compare amounts at two different times. Track changes over time (e.g. “before” and “after”).

💡 Tip:

• Draw a table or model: Before → Change → After
• Be careful with words like “more than”, “less than”, or “now”
• Common in 2-point comparison or before-and-after problems

---

🧩 Example Problem:

There were three times as many men as women at the party at first.
After 18 men left and 10 women entered, there were 6 more men than women remaining.
Find the number of men at the party at first.

---

🧠 Step-by-Step Breakdown:

When you see:

• “There were ___ times as many…”
• “Then some left/entered…”
• “Now there are ___ more than…”
  👉 You’re looking at a comparison at two time points, and it’s time to use algebra or model drawing!